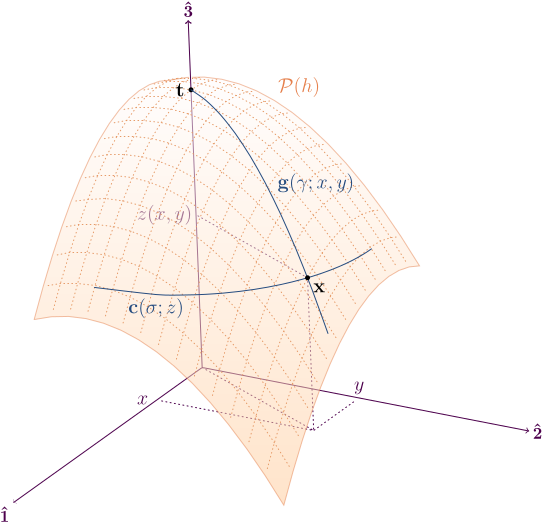
A study of contour and gradient paths
1
on surfaces embedded in ℝ3 is presented.
An interesting formula is introduced for the gradient path
passing over any point of interest in the embedded surface.
A systematic procedure is introduced for calculating both contour
and gradient paths. The surface itself, the contour path, and
the gradient path exist as geometrical objects in their own
right, independent of the choice of coordinates. However, they
admit a specific set of coordinates which seem natural
to the surface. This is studied. The commutitivity of contour
path and gradient path traversal for a flat plane and for an
inverted parabola is analysed.
Download PDF contour+gradient-paths-in-R3.pdf (499 KB)